Non-Linear Shape Optimization Using Local Subspace Projections

Information

• Publication Type: Journal Paper with Conference Talk
• Workgroup(s)/Project(s):
  • MAKE-IT-FAB: Modeling of Shapes for Personal Fabrication
• Date: 2016
• Journal: ACM Transactions on Graphics
• Volume: 35
• Number: 4
• Location: Anaheim, CA, USA
• Lecturer:
  • Przemyslaw Musialski
  • Christian Hafner
• ISSN: 0730-0301
• Event: ACM SIGGRAPH 2016
• DOI: 10.1145/2897824.2925886
• Conference date: 24. July 2016 – 28. July 2016
• Pages: 87:1 – 87:13

Abstract

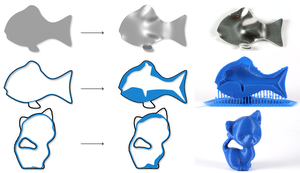
In this paper we present a novel method for non-linear shape optimization of 3d objects given by their surface representation. Our method takes advantage of the fact that various shape properties of interest give rise to underdetermined design spaces implying the existence of many good solutions. Our algorithm exploits this by performing iterative projections of the problem to local subspaces where it can be solved much more efficiently using standard numerical routines.

We demonstrate how this approach can be utilized for various shape optimization tasks using different shape parameterizations. In particular, we show how to efficiently optimize natural frequencies, mass properties, as well as the structural yield strength of a solid body. Our method is flexible, easy to implement, and very fast.

Additional Files and Images

Weblinks

• doi
• DOI: 10.1145/2897824.2925886

BibTeX

@article{musialski_2016_sosp,
  title =      "Non-Linear Shape Optimization Using Local Subspace
               Projections",
  author =     "Przemyslaw Musialski and Christian Hafner and Florian Rist
               and Michael Birsak and Michael Wimmer and Leif Kobbelt",
  year =       "2016",
  abstract =   "In this paper we present a novel method for non-linear shape
               optimization of 3d objects given by their surface
               representation. Our method takes advantage of the fact that
               various shape properties of interest give rise to
               underdetermined design spaces implying the existence of many
               good solutions. Our algorithm exploits this by performing
               iterative projections of the problem to local subspaces
               where it can be solved much more efficiently using standard
               numerical routines.  We demonstrate how this approach can be
               utilized for various shape optimization tasks using
               different shape parameterizations. In particular, we show
               how to efficiently optimize natural frequencies, mass
               properties, as well as the structural yield strength of a
               solid body. Our method is flexible, easy to implement, and
               very fast.",
  journal =    "ACM Transactions on Graphics",
  volume =     "35",
  number =     "4",
  issn =       "0730-0301",
  doi =        "10.1145/2897824.2925886",
  pages =      "87:1--87:13",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2016/musialski_2016_sosp/",
}