Curve Reconstruction with Many Fewer Samples

Information

• Publication Type: Journal Paper with Conference Talk
• Workgroup(s)/Project(s):
  • Harvest4D - Harvesting Dynamic 3D Worlds from Commodity Sensor Clouds
  • Real-Time Shape Acquisition with Sensor-Specific Precision
• Date: 2016
• Journal: Computer Graphics Forum
• Volume: 35
• Number: 5
• Location: Berlin, Germany
• Lecturer: Stefan Ohrhallinger
• ISSN: 1467-8659
• Event: Symposium on Geometry Processing
• Conference date: 20. June 2016 – 24. June 2016
• Pages: 167 – 176
• Keywords: sampling condition, curve reconstruction, curve sampling

Abstract

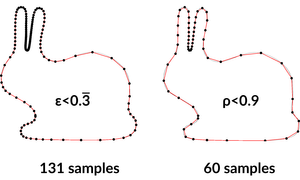
We consider the problem of sampling points from a collection of smooth curves in the plane, such that the Crust family of proximity-based reconstruction algorithms can rebuild the curves. Reconstruction requires a dense sampling of local features, i.e., parts of the curve that are close in Euclidean distance but far apart geodesically. We show that epsilon<0.47-sampling is sufficient for our proposed HNN-CRUST variant, improving upon the state-of-the-art requirement of epsilon<1/3-sampling. Thus we may reconstruct curves with many fewer samples. We also present a new sampling scheme that reduces the required density even further than epsilon<0.47-sampling. We achieve this by better controlling the spacing between geodesically consecutive points. Our novel sampling condition is based on the reach, the minimum local feature size along intervals between samples. This is mathematically closer to the reconstruction density requirements, particularly near sharp-angled features. We prove lower and upper bounds on reach rho-sampling density in terms of lfs epsilon-sampling and demonstrate that we typically reduce the required number of samples for reconstruction by more than half.

Additional Files and Images

Weblinks

• Reproducibility Source Code
  This git repository contains all source code and instructions to reproduce the relevant figures and tables of the paper on an Ubuntu 16.04LTS system.
• doi

BibTeX

@article{ohrhallinger-2016-sgp,
  title =      "Curve Reconstruction with Many Fewer Samples",
  author =     "Stefan Ohrhallinger and Scott A. Mitchell and Michael Wimmer",
  year =       "2016",
  abstract =   "We consider the problem of sampling points from a collection
               of smooth curves in the plane, such that the Crust family of
               proximity-based reconstruction algorithms can rebuild the
               curves. Reconstruction requires a dense sampling of local
               features, i.e., parts of the curve that are close in
               Euclidean distance but far apart geodesically. We show that
               epsilon<0.47-sampling is sufficient for our proposed
               HNN-CRUST variant, improving upon the  state-of-the-art
               requirement of epsilon<1/3-sampling. Thus we may reconstruct
               curves with many fewer samples. We also present a new
               sampling scheme that reduces the required density even
               further than epsilon<0.47-sampling. We achieve this by
               better controlling the spacing between geodesically
               consecutive points. Our novel sampling condition is based on
               the reach, the minimum local feature size along intervals
               between samples. This is mathematically closer to the
               reconstruction density requirements, particularly near
               sharp-angled features. We prove lower and upper bounds on
               reach rho-sampling density in terms of lfs epsilon-sampling
               and demonstrate that we typically reduce the required number
               of samples for reconstruction by more than half. ",
  journal =    "Computer Graphics Forum",
  volume =     "35",
  number =     "5",
  issn =       "1467-8659",
  pages =      "167--176",
  keywords =   "sampling condition, curve reconstruction, curve sampling",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2016/ohrhallinger-2016-sgp/",
}