Reduced-Order Shape Optimization Using Offset Surfaces

Information

• Publication Type: Journal Paper with Conference Talk
• Workgroup(s)/Project(s):
  • MAKE-IT-FAB: Modeling of Shapes for Personal Fabrication
• Date: August 2015
• Journal: ACM Transactions on Graphics (ACM SIGGRAPH 2015)
• Volume: 34
• Number: 4
• Location: Los Angeles, CA, USA
• Lecturer: Przemyslaw Musialski
• ISSN: 0730-0301
• Event: ACM SIGGRAPH 2015
• DOI: 10.1145/2766955
• Conference date: 9. August 2015 – 13. August 2015
• Pages: 102:1 – 102:9
• Keywords: reduced-order models, shape optimization, computational geometry, geometry processing, physical mass properties

Abstract

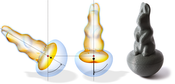
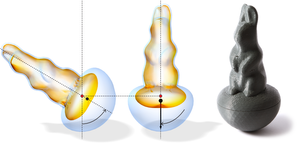
Given the 2-manifold surface of a 3d object, we propose a novel method for the computation of an offset surface with varying thickness such that the solid volume between the surface and its offset satisfies a set of prescribed constraints and at the same time minimizes a given objective functional. Since the constraints as well as the objective functional can easily be adjusted to specific application requirements, our method provides a flexible and powerful tool for shape optimization. We use manifold harmonics to derive a reduced-order formulation of the optimization problem, which guarantees a smooth offset surface and speeds up the computation independently from the input mesh resolution without affecting the quality of the result. The constrained optimization problem can be solved in a numerically robust manner with commodity solvers. Furthermore, the method allows simultaneously optimizing an inner and an outer offset in order to increase the degrees of freedom. We demonstrate our method in a number of examples where we control the physical mass properties of rigid objects for the purpose of 3d printing.

Additional Files and Images

Weblinks

• http://dl.acm.org/citation.cfm?id=2766955
• DOI: 10.1145/2766955

BibTeX

@article{musialski-2015-souos,
  title =      "Reduced-Order Shape Optimization Using Offset Surfaces",
  author =     "Przemyslaw Musialski and Thomas Auzinger and Michael Birsak
               and Michael Wimmer and Leif Kobbelt",
  year =       "2015",
  abstract =   "Given the 2-manifold surface of a 3d object, we propose a
               novel method for the computation of an offset surface with
               varying thickness such that the solid volume between the
               surface and its offset satisfies a set of prescribed
               constraints and at the same time minimizes a given objective
               functional. Since the constraints as well as the objective
               functional can easily be adjusted to specific application
               requirements, our method provides a flexible and powerful
               tool for shape optimization. We use manifold harmonics to
               derive a reduced-order formulation of the optimization
               problem, which guarantees a smooth offset surface and speeds
               up the computation independently from the input mesh
               resolution without affecting the quality of the result. The
               constrained optimization problem can be solved in a
               numerically robust manner with commodity solvers.
               Furthermore, the method allows simultaneously optimizing an
               inner and an outer offset in order to increase the degrees
               of freedom. We demonstrate our method in a number of
               examples where we control the physical mass properties of
               rigid objects for the purpose of 3d printing. ",
  month =      aug,
  journal =    "ACM Transactions on Graphics (ACM SIGGRAPH 2015)",
  volume =     "34",
  number =     "4",
  issn =       "0730-0301",
  doi =        "10.1145/2766955",
  pages =      "102:1--102:9",
  keywords =   "reduced-order models, shape optimization, computational
               geometry, geometry processing, physical mass properties",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2015/musialski-2015-souos/",
}