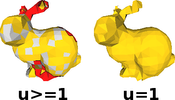Minimizing Edge Length to Connect Sparsely Sampled Unorganized Point Sets

Information

• Publication Type: Journal Paper with Conference Talk
• Workgroup(s)/Project(s):
  • Rendering and Modeling
• Date: October 2013
• Journal: Computers & Graphics (Proceedings of Shape Modeling International 2013)
• Volume: 37
• Number: 6
• Location: Bournemouth, UK
• Lecturer: Stefan Ohrhallinger
• ISSN: 0097-8493
• Event: Shape Modeling International 2013 (SMI)
• Conference date: 10. July 2013 – 12. July 2013
• Pages: 645 – 658
• Keywords: point cloud, reconstruction

Abstract

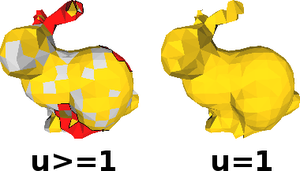
Most methods for interpolating unstructured point clouds handle densely sampled point sets quite well but get into trouble when the point set contains regions with much sparser sampling, a situation often encountered in practice. In this paper, we present a new method that provides a better interpolation of sparsely sampled features. We pose the surface construction problem as finding the triangle mesh which minimizes the sum of all triangles’ longest edge. The output is a closed manifold triangulated surface Bmin. Exact computation of Bmin for sparse sampling is most probably NP-hard, and therefore we introduce suitable heuristics for its computing. The algorithm first connects the points by triangles chosen in order of their longest edge and with the requirement that all edges must have at least 2 incident triangles. This yields a closed non-manifold shape which we call the Boundary Complex. Then we transform it into a manifold triangulation using topological operations. We show that in practice, runtime is linear to that of the Delaunay triangulation of the points.

Additional Files and Images

Weblinks

No further information available.

BibTeX

@article{ohrhallinger_stefan-2013-smi,
  title =      "Minimizing Edge Length to Connect Sparsely Sampled
               Unorganized Point Sets",
  author =     "Stefan Ohrhallinger and Sudhir Mudur and Michael Wimmer",
  year =       "2013",
  abstract =   "Most methods for interpolating unstructured point clouds
               handle densely sampled point sets quite well but get into
               trouble when the point set contains regions with much
               sparser sampling, a situation often encountered in practice.
               In this paper, we present a new method that provides a
               better interpolation of sparsely sampled features. We pose
               the surface construction problem as finding the triangle
               mesh which minimizes the sum of all triangles’ longest
               edge. The output is a closed manifold triangulated surface
               Bmin. Exact computation of Bmin for sparse sampling is most
               probably NP-hard, and therefore we introduce suitable
               heuristics for its computing. The algorithm first connects
               the points by triangles chosen in order of their longest
               edge and with the requirement that all edges must have at
               least 2 incident triangles. This yields a closed
               non-manifold shape which we call the Boundary Complex. Then
               we transform it into a manifold triangulation using
               topological operations. We show that in practice, runtime is
               linear to that of the Delaunay triangulation of the points.",
  month =      oct,
  journal =    "Computers & Graphics (Proceedings of Shape Modeling
               International 2013)",
  volume =     "37",
  number =     "6",
  issn =       "0097-8493",
  pages =      "645--658",
  keywords =   "point cloud, reconstruction",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2013/ohrhallinger_stefan-2013-smi/",
}