Die Cusp-Bifurkation
Wie schon bei der Hopf-Bifurkation, so wird auch die
Cusp-Bifurkation durch eine entsprechende Singularität gekennzeichnet.
Zur Untersuchung dieser Cusp-Singularität wenden wir ein neues
Verfahren an, das sogenannt Blowing-Up. Diese Methode wird verwendet,
um nicht-hyperbolische Fixpunkt zu untersuchen. Der Fixpunkt wird dabei
mittels Koordinatentransformationen zu einer Kurve "aufgeblasen" (daher der
Name "Blowing-Up"), welche eine Reihe von Singularitäten enthält.
Die einfachste Form verwendet die Transformation in Polarkoordinaten, und
heißt daher auch
polares Blowing-Up.
Die Singularitäten der Cusp-Bifurkation lassen sich ebenfalls wieder
durch Blowing-Up berechnen. Von Interesse ist hierbei die
Cusp-Singularität,
bei der, der Fixpunkt eine Spitze (Cusp) ausbildet.
Betrachten wir als einfaches Beispiel die Differentialgleichung
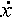 = p1 + p2x - x3
Wir wollen nun im (p1/p2/x)-Raum die
Mannigfaltigkeit
= p1 + p2x - x3
Wir wollen nun im (p1/p2/x)-Raum die
Mannigfaltigkeit
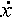 betrachten. Diese Mannigfaltigkeit ist in
Abbildung 15
dargestellt (der besseren Übersicht wegen ist sie jedoch in die
positive x-Achsenrichtung verschoben worden). Bei näherer Betrachtung
fällt auf, daß es einen Bereich in der
(p1/p2)-Ebene mit einem und einen mit drei Equilibria
gibt. Wenn man, um von einem Punkt auf der Mannigfaltigkeit zu einem anderen
zu kommen, einen "Sprung" durchführen muß, ist es aber nun
möglich, durch geschicktes Umfahren der Singularität diesem
"Sprung" auszuweichen (vergleiche dazu die beiden Linien auf der
Mannigfaltigkeit in der Abbildung).
betrachten. Diese Mannigfaltigkeit ist in
Abbildung 15
dargestellt (der besseren Übersicht wegen ist sie jedoch in die
positive x-Achsenrichtung verschoben worden). Bei näherer Betrachtung
fällt auf, daß es einen Bereich in der
(p1/p2)-Ebene mit einem und einen mit drei Equilibria
gibt. Wenn man, um von einem Punkt auf der Mannigfaltigkeit zu einem anderen
zu kommen, einen "Sprung" durchführen muß, ist es aber nun
möglich, durch geschicktes Umfahren der Singularität diesem
"Sprung" auszuweichen (vergleiche dazu die beiden Linien auf der
Mannigfaltigkeit in der Abbildung).
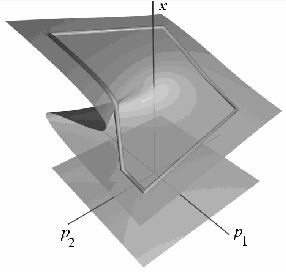
Abbildung 15:
Eine Mannigfaltigkeit für die Cusp-Bifurkation der
Differentialgleichung
p1 + p2x - x3
(; die Mannigfaltigkeit ist in positiver x-Richtung verschoben, der
Ursprung liegt eigentlich im Durchstoßpunkt von Mannigfaltigkeit und
x-Achse). Unterhalb der Mannigfaltigkeit sind die Bereiche mit je einem
bzw. drei Equilibria abgebildet.
[<= Subcritical Hopf-Bifurkation]
[== Cusp-Bifurkation]
[=> Flip-Bifurkation]
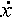 = p1 + p2x - x3
= p1 + p2x - x3
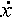 = p1 + p2x - x3
= p1 + p2x - x3
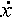 betrachten. Diese Mannigfaltigkeit ist in
Abbildung 15
dargestellt (der besseren Übersicht wegen ist sie jedoch in die
positive x-Achsenrichtung verschoben worden). Bei näherer Betrachtung
fällt auf, daß es einen Bereich in der
(p1/p2)-Ebene mit einem und einen mit drei Equilibria
gibt. Wenn man, um von einem Punkt auf der Mannigfaltigkeit zu einem anderen
zu kommen, einen "Sprung" durchführen muß, ist es aber nun
möglich, durch geschicktes Umfahren der Singularität diesem
"Sprung" auszuweichen (vergleiche dazu die beiden Linien auf der
Mannigfaltigkeit in der Abbildung).
betrachten. Diese Mannigfaltigkeit ist in
Abbildung 15
dargestellt (der besseren Übersicht wegen ist sie jedoch in die
positive x-Achsenrichtung verschoben worden). Bei näherer Betrachtung
fällt auf, daß es einen Bereich in der
(p1/p2)-Ebene mit einem und einen mit drei Equilibria
gibt. Wenn man, um von einem Punkt auf der Mannigfaltigkeit zu einem anderen
zu kommen, einen "Sprung" durchführen muß, ist es aber nun
möglich, durch geschicktes Umfahren der Singularität diesem
"Sprung" auszuweichen (vergleiche dazu die beiden Linien auf der
Mannigfaltigkeit in der Abbildung).