Light Space Perspective Shadow Maps - Pictures and Videos

More Pictures and Videos

Figure 1 from the paper: Light space perspective shadow maps (LiSPSM) (left) and the corresponding warped light view (including the eye frustum) (right). Note the high shadow detail both for near and distant objects.

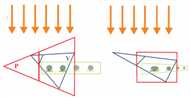Figure 2 from the paper: An example configuration of light space perspective shadow maps with view frustum V and the frustum defining the perspective transform P. Left: Note how the light rays l are parallel to the near and far plane of P. Right: After perspective transformation, the light direction is unchanged.

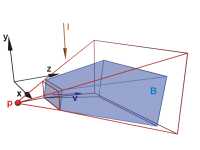Figure 3 from the paper: Construction of the perspective frustum P in 3D.

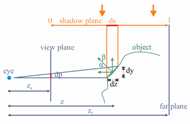Figure 4 from the paper: Aliasing in shadow mapping.

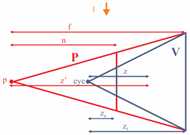Figure 5 from the paper: The parameterization of light space perspective shadow maps (shows the yz-plane in light space). The parameter n is free and can vary between zn (perspective shadow mapping) and infinity (uniform shadow mapping).

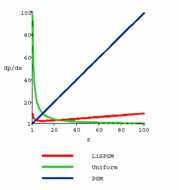Figure 6 from the paper: Perspective aliasing errors plotted against z-coordinate for different shadow mapping techniques.

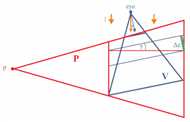Figure 7 from the paper: The z-range affected by the reparameterization is small when the view direction gets near the light direction. For perspective shadow maps, V and P would be identical, but the effect of the warp on the z-distribution would be the same.

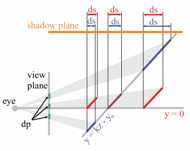Figure 8 from the paper: Shows the lines along which the perspective error is analyzed. PSMs have constant error on small edges along the sloped line, whereas LiSPSMs distribute error evenly for small edges along the line with y = 0. The warping effect for PSMs is much stronger, which is in general not desirable.

Clip 1 changing the free parameter n (2MB, 512x512, DivX)

Clip 2 changing the free parameter n (2MB, 512x512, DivX)

Clip 3 changing the free parameter n (2MB, 512x512, DivX)

Clip 4 changing the free parameter n (3MB, 512x512, DivX)

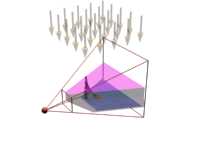Clip 5 How to calculate the intersection body B (16MB, 640x480, DivX)