Algorithmic Botany via Lindenmayer Systems in Blender

Information

• Publication Type: Bachelor Thesis
• Workgroup(s)/Project(s):
  • Rendering and Modeling
• Date: August 2017
• Date (Start): 4. March 2016
• Date (End): 9. August 2017
• Matrikelnummer: 1327344
• First Supervisor: Michael Wimmer
• Keywords: l-systems, algorithmic botany

Abstract

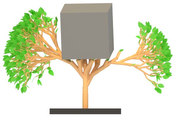
Lindenmayer systems, or L-systems, are a well-established and thoroughly studied concept in the field of computer graphics. Originally introduced by theoretical botanist Aristid Lindenmayer to model the development of simple multicellular organisms, they are now commonly associated with the modeling of whole plants and complex branching structures. Various extensions such as stochastic, parametric and context-sensitive L-systems have been introduced to the formalism, allowing the modeling of stochastic, continuous growth and complex interactions of plant organisms with each other and with the external environment. More specialized interactive techniques are arguably better suited to more intuitively and predictably produce plant structures where artistic control is essential. Nonetheless, L-systems remain a fascinating and powerful methodology as they allow for the description of patterns of astonishing diversity via simple formal rules of production and graphical interpretation of the results. Small changes to these rules often yield unexpected but aesthetically fascinating results and the plethora of forms and patterns thus produced constitute a subject of study that is highly worthwhile in itself.

The focus of this work is not to present novel techniques for the aesthetic or biological modeling of plants. This work aims at integrating the existing formalism of parametric, context-sensitive L-systems in a widely used open-source computer graphics software like Blender in the form of an add-on, as well as to discuss the potential advantages of such an integration. In this regard, special consideration is given to allow the modeling of environmental interaction of a growing structure with a Blender scene.

Additional Files and Images

Weblinks

• Source code repository

BibTeX

@bachelorsthesis{LEOPOLD-2017-ALG,
  title =      "Algorithmic Botany via Lindenmayer Systems in Blender",
  author =     "Nikole Leopold",
  year =       "2017",
  abstract =   "Lindenmayer systems, or L-systems, are a well-established
               and thoroughly studied concept in the field of computer
               graphics. Originally introduced by theoretical botanist
               Aristid Lindenmayer to model the development of simple
               multicellular organisms, they are now commonly associated
               with the modeling of whole plants and complex branching
               structures. Various extensions such as stochastic,
               parametric and context-sensitive L-systems have been
               introduced to the formalism, allowing the modeling of
               stochastic, continuous growth and complex interactions of
               plant organisms with each other and with the external
               environment. More specialized interactive techniques are
               arguably better suited to more intuitively and predictably
               produce plant structures where artistic control is
               essential. Nonetheless, L-systems remain a fascinating and
               powerful methodology as they allow for the description of
               patterns of astonishing diversity via simple formal rules of
               production and graphical interpretation of the results.
               Small changes to these rules often yield unexpected but
               aesthetically fascinating results and the plethora of forms
               and patterns thus produced constitute a subject of study
               that is highly worthwhile in itself.  The focus of this work
               is not to present novel techniques for the aesthetic or
               biological modeling of plants. This work aims at integrating
               the existing formalism of parametric, context-sensitive
               L-systems in a widely used open-source computer graphics
               software like Blender in the form of an add-on, as well as
               to discuss the potential advantages of such an integration.
               In this regard, special consideration is given to allow the
               modeling of environmental interaction of a growing structure
               with a Blender scene.",
  month =      aug,
  address =    "Favoritenstrasse 9-11/E193-02, A-1040 Vienna, Austria",
  school =     "Institute of Computer Graphics and Algorithms, Vienna
               University of Technology ",
  keywords =   "l-systems, algorithmic botany",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2017/LEOPOLD-2017-ALG/",
}