Migration of Surface Curve to Most Concave Isoline

Information

• Publication Type: Bachelor Thesis
• Workgroup(s)/Project(s):
  • Harvest4D - Harvesting Dynamic 3D Worlds from Commodity Sensor Clouds
• Date: December 2016
• Date (Start): July 2016
• Date (End): December 2016
• Matrikelnummer: e0926916
• First Supervisor: Michael Wimmer

Abstract

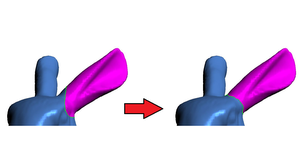
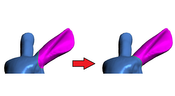
In this paper, I present a solution for migrating a curve on a three dimensional surface to the most concave isoline in its vicinity. Essentially, this problem statement tackles mesh segmentation from a different angle. The search for a suitable segmentation boundary is reduced to a shortest path problem. First, a graph is built using the mesh’s vertices and edges near the input curve. Then, the shortest path is found using the Dijkstra algorithm, whereas a modified weighting scheme that makes the passing through of concave edges cheaper, among other factors, results in a path suitable as segmentation boundary. The final algorithm provides segmentation boundaries of a quality similar to existing segmentation algorithms. The runtime generally lies below a second, thus making it viable for on the go optimization of the user’s input.

Additional Files and Images

Weblinks

No further information available.

BibTeX

@bachelorsthesis{Mayrhauser-2016-Cnc,
  title =      "Migration of Surface Curve to Most Concave Isoline",
  author =     "Maximilian Mayrhauser",
  year =       "2016",
  abstract =   "In this paper, I present a solution for migrating a curve on
               a three dimensional surface to the most concave isoline in
               its vicinity. Essentially, this problem statement tackles
               mesh segmentation from a different angle. The search for a
               suitable segmentation boundary is reduced to a shortest path
               problem. First, a graph is built using the mesh’s vertices
               and edges near the input curve. Then, the shortest path is
               found using the Dijkstra algorithm, whereas a modified
               weighting scheme that makes the passing through of concave
               edges cheaper, among other factors, results in a path
               suitable as segmentation boundary. The final algorithm
               provides segmentation boundaries of a quality similar to
               existing segmentation algorithms. The runtime generally lies
               below a second, thus making it viable for on the go
               optimization of the user’s input.",
  month =      dec,
  address =    "Favoritenstrasse 9-11/E193-02, A-1040 Vienna, Austria",
  school =     "Institute of Computer Graphics and Algorithms, Vienna
               University of Technology ",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2016/Mayrhauser-2016-Cnc/",
}