Saddles im 3d

Damit ein Fixpunkt ein Saddle ist, muß es Eigenwerte geben, deren Realteile positiv und andere deren Realteile negativ sind. Daher sind im 3d folgende Kombinationen denkbar:

1. ein reeller positiver und zwei konjugiert komplexe Eigenwerte (mit neg. Realteil)

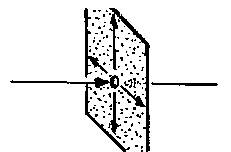
   In einer Ebene des lokalen linearisierten Systems liegt ein spiralförmiger Attraktor. Das erkennt man an den beiden konjugiert komplexen Eigenwerten, deren Realteil negativ ist. Nun denkt man sich einen Repellor - keinen spiralförmigen, weil der Eigenwert reell ist - dazu. Dann ergibt sich eigentlich automatisch, ohne viel überlegen zu müssen, der folgende Saddle:

   

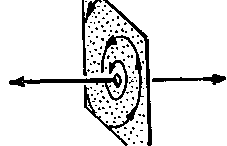
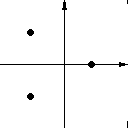
   Bei dieser Art von Saddle existiert sicherlich eine invariante Fläche. Das heißt, daß Punkte, die in dieser Fläche (des spiralförmigen Attraktors) liegen, diese niemals verlassen. Alle anderen Punkte nähern sich zwar anfangs dem Fixpunkt, entfernen sich aber gleichzeitig immer mehr von der Fläche. Diese Punkte ziehen immer enger werdende Kreise um jene Kurve k₁ "entlang" der sie sich von F entfernen.

2. ein reeller positiver und zwei reelle negative Eigenwerte

   Der positive Eigenwert beschreibt eine Kurve, die den Fixpunkt verläßt. Selbstverständlich wird nicht wirklich der Fixpunkt verlassen - sonst wäre der Fixpunkt nicht fix, sondern nur Punkte die sehr, sehr nahe an F liegen, entfernen sich. Die negativen Eigenwerte beschreiben Kurven, entlang denen sich Punkte dem Fixpunkt nähern.

   

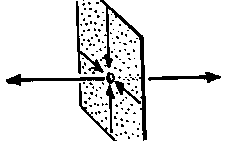
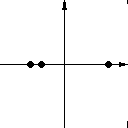
   Eigentlich interessant sind jedoch nicht die Punkte, die auf einer dieser Kurven liegen, sondern alle anderen. Stellvertretend für alle Punkte sind die im Bild dargestellten Trajektorien. Bemerkenswert sind Punkte die in der Ebene der beiden anziehenden Kurven liegen; diese Punkte entfernen sich niemals von der Ebene. Sie nähern sich lediglich F an, erreichen den Fixpunkt aber auch niemals (theoretisch).

3. zwei reelle positive und ein reeller negativer Eigenwert

   Dieser Punkt ist im wesentlichen analog zum soeben besprochenen und nur der Vollständigkeit halber angeführt. Die "Annäherungskurven" sind nun "Abstoßungskurven" und vice versa. Lediglich die Orientierung der Pfeile wurde umgedreht.

   

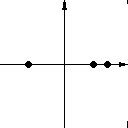
   Natürlich hat sich damit auch die Orientierung der Trajektorien verändert. Acht geben muß man allerdings bei einer Slow-Fast Dynamik , denn die "langsamen" Kurven werden zu schnellen und umgekehrt.

4. ein reeller negativer und zwei konjugiert komplexe Eigenwerte (mit pos. Realteil)

   Dieser Punkt ist Fall 1 sehr ähnlich. Es sind wiederum nur Anziehung und Abstoßung miteinander vertauscht.

   

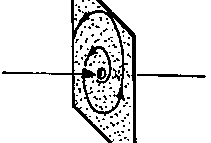
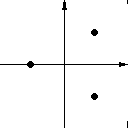
   Die Ebene, in der sich die (abstoßende) Spirale befindet ist genauso wie die zuvor beschriebene invariant.