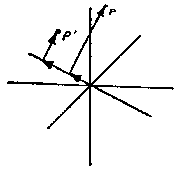
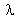i
und Eigenvektoren xi der Matrix f'|x=F aus
der Gleichung f'|x=Fxi=
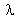ixi bzw.
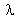det(f'|x=F-;E)=0 bestimmen.
Diese beschreiben kurz und prägnant (wie
wir später noch sehen werden), aber vollständig das Verhalten
nahe F.
[Tson92]
Man kann die
Eigenwerte
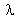i
und Eigenvektoren xi der Matrix f'|x=F aus
der Gleichung
f'|x=Fxi=
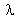ixi bzw.
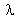det(f'|x=F-;E)=0 bestimmen.
Diese beschreiben kurz und prägnant (wie
wir später noch sehen werden), aber vollständig das Verhalten
nahe F.
[Tson92]
Die reellen Eigenvektoren bestimmen n (hier 2) Geraden durch den Ursprung eines lokalen Koordinatensystems in F :
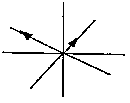
Punkte die auf einer dieser Geraden liegen, werden die Gerade auch in den folgenden Zeitschritten niemals verlassen. Es sei nochmals betont, daß wir nun ein lokales System mit F im Ursprung (bei der Taylorentwicklung haben wir lediglich die linearen Terme berücksichtigt) geschaffen haben, das uns zur Analyse des Verhaltens in der Nähe eines gegebenen Fixpunktes dient.
Die Eigenwerte bestimmen nun, ob sich ein auf einer Geraden liegender Punkt dem Ursprung nähert oder sich entfernt. Negative Eigenwerte bedeuten eine Kontraktion des Eigenvektors und damit ein Annähern an den Ursprung, während ein positiver Eigenwert genau das Gegenteil bedeutet.
Das im vorigen Absatz Erwähnte gilt genau dann, wenn die Eigenwerte reell sind. Sollte man komplexe Eigenwerte erhalten, dann sagt das Vorzeichen des Realteils, wie bei rein reellen Eigenwerten, aus, ob sich die Punkte nähern oder entfernen. Allerdings ergibt sich bei komplexen Eigenwerten eine spiralförmige Bewegung. Je größer der Betrag des Imaginärteils ist, desto höher ist die Rotationsgeschwindigkeit um den Punkt.
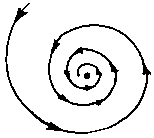
Nimmt man nun wie in der folgenden Abbildung gezeigt in diesem lokalen Koordinatensystem einen Punkt an, der auf keiner der beiden Geraden liegt, dann kann man sein Verhalten folgendermaßen beschreiben:
Der Ortsvektor p des Punktes wird in n Komponenten (die Eigenvektoren e1, e2, ...,en . p=a1e1+a2e2+ ...+anen) zerlegt. Anschließend werden die Eigenvektoren entsprechend den Eigenwerten gestreckt oder gestaucht. Nun kann die neue Lage des Punktes wieder durch die Addition (Linearkombination) der modifizierten Eigenvektoren (mit den n gleichgebliebenen Skalaren a1, a2, ... , an multipliziert) bestimmt werden. Hier muß nochmals betont werden ,daß dies nur in der Nähe von F gilt, weil f ja linearisiert wurde.
