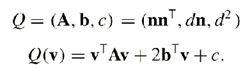Geometry over Network
Techniques:
Mesh Simplification and
Multiresolution Data Structures
Markus Hadwiger
msh@cg.tuwien.ac.at
Institute of
Computer Graphics
Vienna University
of Technology
Vienna / Austria
Introduction
The transmission of a non-trivial amount of geometry data over a network
has a lot of applications. First, data that is not available locally may
need to be downloaded in order to be viewed and used. To avoid extremely
lengthy transmission times some kind of compression technique should be
employed. Special techniques for geometry compression have been developed
for this purpose. The problem gets worse when data needs to be sent continuously,
say, because it is being generated dynamically by the server. Apart from
compression there is also the issue of simplification. With simplification
the primary aim is not to compress geometry in its original resolution,
but to generate one or more simplified versions of a geometric model. These
can be used to speed up both transmission and rendering times, for instance.
As soon as several levels of resolution, i.e., detail, have been generated
for a model the idea of combining all of these into a single, uniform data
structure seems very worthwhile. Such multiresolution data structures can
be used to transmit geometry progressively over a network, render at a
level of detail that is appropriate for the current viewing distance, and
a lot of other applications, like multiresolution editing.
This document contains material I used for my research seminar talk
on January 13, 1999. The topic of this talk was mesh simplification and
multiresolution data structures, and their utility to the transmission
of geometry data over networks.
Acknowledgments
I have used images from [Gar97], [Gar98],
[Hop96],
and [Hop98] to illustrate the two case studies of Quadric
Error Metrics and Progressive Meshes, respectively.
Contents
1. Problem Statement
2. Overview of Methods
3. Classification of Algorithms
4. Case Studies
4.1 Case Study #1: Generation (Quadric Error Metrics)
4.2 Case Study #2: Representation (Progressive Meshes)
5. References
1. Problem Statement
Highly detailed geometric models need to be:
• rendered
• stored
• transmitted
There are also a lot of other uses for mesh simplification and multiresolution
data structures, like collision detection at a different resolution than
the one use for rendering, editing a model not in its highest resolution,
but at an arbitrary level of detail, automatically applying the changes
to the entire multiresolution structure, and so on.
2. Overview of Methods
Over the past several years a tremendous amount of work has been done on
mesh simplification and multiresolution data structures and editing. The
following list contains some of the work that has been very important and
influential, being representative for a distinct approach to tackle the
problem.
• Vertex Clustering [Ros93]
Group vertices into clusters and determine a single representative
vertex. Iteratively merge clusters into larger clusters until only a single
cluster/vertex remains. Clustering by simple coordinate quantization, octrees,
...
+ fast and simple.
- often very bad output quality.
- degree of simplification only controllable indirectly (quantization
parameters).
• Decimation [Sch92]
Very early work on Mesh Decimation. Iteratively remove vertices
that pass a certain distance/angle criterion. Patch resulting holes by
local retriangulation. Primarily developed for processing output of Marching
Cubes.
• Edge Collapse [Hop93]
Mesh Optimization paper. Vertices connected by an edge are
collapsed into a single representative vertex. This is the most often used
primitive operation! Efficiency depends on the error metric employed.
• Re-Tiling [Tur92]
Distribute entirely new set of vertices over the surface of
the model. Best suited to curved surfaces, bad for models with sharp corners
and edges. Few other restrictions on the model (may have holes, ...). Points
are placed by point repulsion and then connected together.
• Wavelets [Gro96]
Requires regular, hierarchical decomposition (e.g., regularly
gridded meshes). Multiresolution for free! Very good results, but not very
fast.
3. Classification of Algorithms
There are a lot of criteria that can be used to classify the huge number
of approaches and algorithms, like whether an algorithm is able to operate
on arbitrary topology, produces manifold or non-manifold output, is only
able to operate on height-fields, and so on:
-
triangle meshes/height-fields
-
vertex subset/resampling
-
manifold/non-manifold surfaces
-
topology altering/preserving
-
error metric
-
specify error bound or mesh detail
-
multiresolution or discrete LOD
Mesh Decimation and Mesh Optimization (edge collapse) approaches generally
preserve mesh topology, whereas Vertex Clustering does not.
Vertex subsets are used by Mesh Decimation, whereas vertices are re-sampled
by Mesh Optimization and Re-Tiling.
4. Case Studies
The following section contains two case studies. First, Quadric Error Metrics
[Gar97]
uses an error metric that combines computational efficiency and high quality
results. Second, Progressive Meshes [Hop96] introduces
a format for efficient representation of a mesh in a progressive multiresolution
data structure.
4.1 Case Study #1: Generation (Quadric
Error Metrics)
"Surface Simplification Using Quadric Error Metrics", introduced at SIGGRAPH
1997 by Michael Garland and Paul S. Heckbert [Gar97]
uses a remarkable error metric that can be used for efficient generation
of multiple levels of detail for a given triangle mesh of arbitrary topology.
Surface properties have been integrated into their original approach later
on [Gar98].
Edge Contraction
The basic primitive for simplification is the edge contraction:
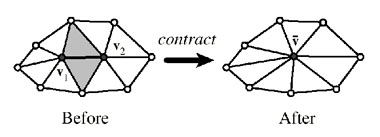
Figure 1: edge contraction
Whenever two vertices have to be contracted a new representative vertex
has to be chosen:
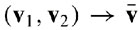
There are two different approaches: subset placement (one of the two
original vertices is used), and optimal placement (a new vertex position
is synthesized).
Quadric Error: Contraction Cost
The squared distance of a point to a plane is fundamental to the calculation
of the cost (error introduced) of edge contractions:
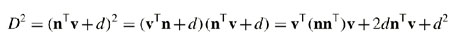
A quadric (represented by a symmetric, positive semi-definite matrix
Q) is associated with each vertex, subsuming the sum of the squared distances
of the vertex to all its incident planes:
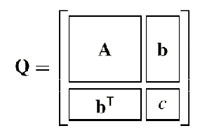
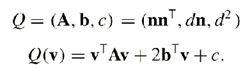
Figure 2: Structure of quadric matrix and error calculation of a single
vertex
Algorithm Overview
1. Compute Q for all vertices
2. Choose valid pairs
3. Compute optimal targets and costs
4. Place pairs in heap (root==min-cost)
5. Contract root, update participants
6. goto 5 if goal not yet reached
Quadric Isosurfaces
Quadric Error Metrics have a nice geometric interpretation. Each quadric
corresponds to a quadric surface centered at the point of minimal error.
The surface itself (an ellipsoid in the non-degenerate case) has the same
error everywhere, that is, it is an isosurface for a given error.
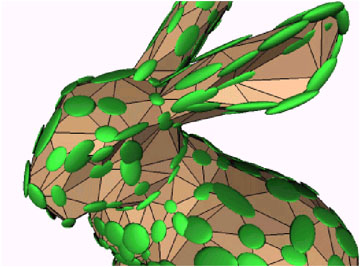
Figure 3: non-degenerate quadric isosurfaces (ellipsoids)
Boundary Constraints
To prevent destruction of boundaries invisible orthogonal planes with large
penalty have to be added to boundary edges:
Figure 4: orthogonal boundary plane
For example, a cylinder without caps would be teared apart by the algorithm,
if no boundary constraints (planes) are used:
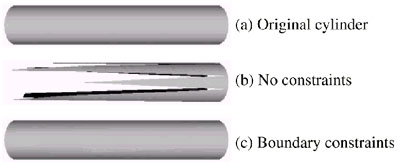
Figure 5: preventing destruction of boundaries
Surface Properties
Addition of surface properties to the algorithm:
-
surface normals
-
colors (linearly interpolated)
-
textures (texture coordinates)
The integration of surface properties is the n-dimensional extension of
the original approach for geometry.
Still, there is a huge problem with attribute discontinuities, especially
if there are a lot of them!
See [Gar98].
Preserving Discontinuities
Attribute discontinuities can be preserved by introducing boundary planes
in n-dimensional space, analogously to the preservation of geometric boundaries
in the 3-dimensional case:
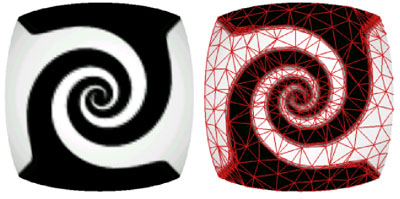
Figure 6: preserving discontinuity curves
4.2 Case Study #2: Representation (Progressive
Meshes)
"Progressive Meshes", SIGGRAPH 1996, by Hugues Hoppe [Hop96]
introduced a very efficient data structure that can be used to represent
a triangle mesh at multiple levels of detail, also allowing progressive
refinement and transmission. This paper also introduced a very high quality
error metric using energy functions. Another paper by the same author focuses
exclusively on the progressive mesh format [Hop98]
and how to use it efficiently.
Basic Idea
-
Construct multiresolution representation by iteratively performing edge
collapses.
-
Store the simplified mesh (base mesh) along with the inverse of all performed
edge collapses (vertex splits).
-
Inherently progressive (transmission, ...)
PM Representation
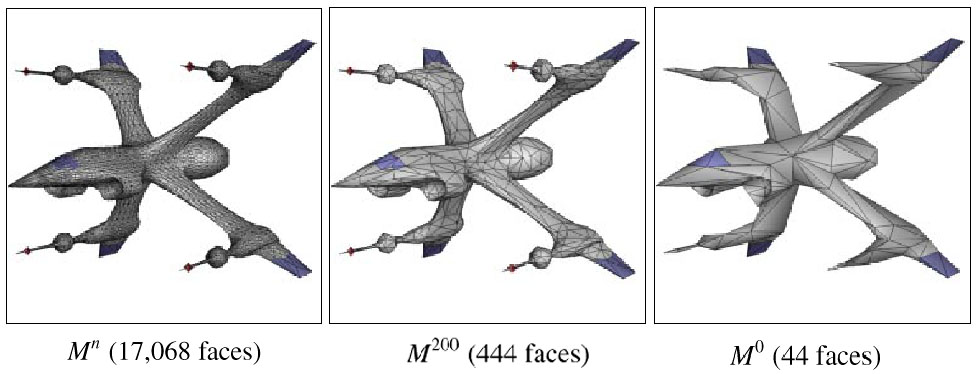
Figure 7: From original mesh to base mesh
The base mesh has the lowest resolution and can be refined progressively
by iteratively applying vertex splits, the inverse operation of edge collapses:
Vertices, Corners, and Wedges
Two different kinds of attributes have to be distinguished:
-
discrete (face attributes)
-
scalar (vertex attributes)
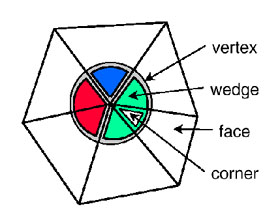
Figure 8: vertices, wedges, corners
Because of discontinuities scalars have to be associated with corners.
A corner is a (vertex,face) pair.
What do we need to store?
The following information needs to be stored in a progressive mesh:
| geometry: |
{v1}: ( x, y, z ) |
|
{v2}: ( x, y, z ) |
|
|
| connectivity: |
{f1}: { v1, v2, v3 } |
|
{f2}: { v3, v2, v1 } |
|
|
| face attributes: |
{f1}: material (shader) |
|
|
| corner attributes: |
{ f1, v1 }: (u,v) ( nx, ny, nz ) |
|
{ f2, v1 }: (u,v) ( nx, ny, nz ) |
Geomorphs
In order to perform smooth visual transitions between different levels
of detail geomorphs can be performed. The ancestor vertex of a set of vertices
is determined and all vertices are interpolated between ancestor and destination
position.
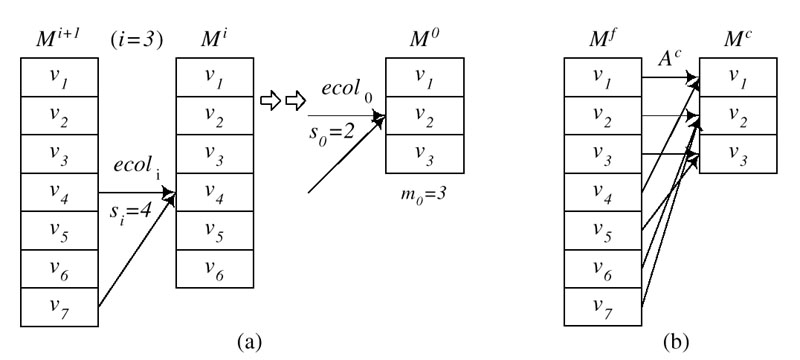
Figure 9: Ancestor tracking for geomorphs
Relation to Geometry Compression
Normally multiresolution representations need more space than a single
resolution, because not only the original mesh needs to be stored, but
also additional information for all other levels of detail.
However, if the only mesh stored in its entirety is the lowest-resolution
mesh and all other levels are stored as deltas from the base-mesh it can
also be used for compression: delta encoding. At least, the storage requirements
of a multiresolution representation need not be higher than storing a high-resolution
mesh.
-
Base mesh is typically very small.
-
Vertex split encoding must be efficient!
5. References
| [Cig98] |
P. Cignoni, C. Montani, and R. Scopigno. A Comparison of Mesh Simplification
Algorithms. In Computers & Graphics Vol.22, No.1 (1998). pp. 37-54. |
| [Gar97] |
Michael Garland and Paul S. Heckbert. Surface Simplification using
Quadric Error Metrics. In SIGGRAPH '97 Conference Proceedings (1997). pp.
209-216. |
| [Gar98] |
Michael Garland and Paul S. Heckbert. Simplifying Surfaces with Color
and Texture using Quadric Error Metrics. In Visualization '98 Proceedings
(1998). |
| [Gro96] |
Markus Gross, O. Staadt, and R. Gatti. Efficient Triangular Surface
Approximations using Wavelets and Quadtree Structures. IEEE Transactions
on Visual and Computer Graphics, 2(2) (1996). pp.130-144. |
| [Hop93] |
Hugues Hoppe, Tony DeRose, Tom Duchamp, John McDonald, and Werner Stuetzle.
Mesh Optimization. In SIGGRAPH ’93 Conference Proceedings (1993). pp. 19-26. |
| [Hop96] |
Hugues Hoppe. Progressive Meshes. In SIGGRAPH '96 Conference Proceedings
(1996). pp. 99-108. |
| [Hop98] |
Hugues Hoppe. Efficient Implementation of Progressive Meshes.
In Computers & Graphics Vol.22, No.1 (1998). |
| [Ros93] |
Jarek Rossignac and P. Borrel. Multi-resolution 3D Approximation for
Rendering Complex Scenes. In Geometric Modeling in Computer Graphics. Springer
Verlag, 1993. pp. 455-465. |
| [Ros96] |
Jarek Rossignac. Geometric Simplification. In SIGGRAPH '96 Course Notes
No.35 (1996). |
| [Sch92] |
William J. Schroeder, Jonathan A. Zarge, and William E. Lorensen. Decimation
of Triangle Meshes. In SIGGRAPH ’92 Conference Proceedings (1992). pp.
65-70. |
| [Tur92] |
Greg Turk. Re-Tiling Polygonal Surfaces. In SIGGRAPH ’92 Conference
Proceedings (1992). pp. 55-64. |


![]()