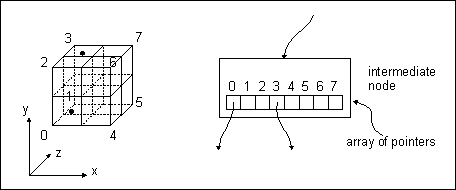
All coordinates stored in a Coordinate3 node will be stored into an
octree with adaptive depth. As the name implies, each node can have a maximum
of eight successors. The nodes in this tree are representing cubic fractions
of space. An intermediate node divides his cube into eight subcubes with
the same size by halving the sides. This means the (max 8) successors of
the intermediate node are representing subcubes of the cube of this node.
The cube parameters are not stored explicit in the nodes, they are definitly
defined by the parameters of the superior cube and the index of the successor
pointer to this cube. A cube defined by a leaf node contains exactly one
coordinate. The insert algorithm creates automatically intermediate nodes
if two coordinates would fall into the same cube.

Each node has an array of pointers to it's successors. As shown in
the picture above an intermediate node divides his cube into eight subcubes.
A subnode of this node with index i represents a subcube with this index
as shown in the left half of the picture. Each leaf node contains exactly
one coordinate. So if two coordinates would fall into the same cube, this
cube must be divided into subcubes using an intermediate node. In the example
in the picture above such an intermediate is shown. The node has two subnodes
(in this case leaf nodes) defining two subcubes 0 and 3 which are containing
a coordinate.
Before any coordinate can be inserted into an octree, the bounds of
all coordinates which are intended to be inserted must be known. These
bounds specify the cube represented by the root-node. In the example below
these bounds are the intervals [0-8], [0-8], [0-8] for x, y and z.

The insert algorithm is realized by a recursive function.
Beginning with the root of the tree the function walks through the
tree.
While the current node is an intermediate node the function calculates
the subcubes and finds out in which subcube the new coordinate is inside.
This determines the right successor for searching again. This is made until
a leaf node is reached or the pointer to the successor is NULL.
Then there are three cases:
This means the algorithm has found a place to insert. The successor pointer will be set to the new node. An example for this case you can see in the picture above.
This means an equal coordinate already exists. The new coordinate will not be inserted into the tree. An example for this case you can see in the picture above.
Two coordinates would fall into the same cube this means the octree
is not deep enough. The leaf node will be replaced by a new intermediate
node. The old leaf node and the new node will be inserted into the new
intermediate node using recursive calls to the function. It can happen
that the two coordinates would fall again into the same cube. In this case
this algorithm would be applied again.
In the picture above the algorithm reaches the leaf node containing
the coordinate (3,1,2). The new coordinate is (3,1,1) so it is different
to (3,1,2). The old leaf node will be replaced by a new intermediate node
and the nodes (3,1,1) and (3,1,2) will be inserted into the new intermediate
node.
For generating LODs it is neccessary to select representatives of clusters
of coordinates. The program uses octree quantization this means the leaves
of the tree will be combined into parent nodes. Each node has an pointer
(called represent) to it's parent node. But if anyone wants to get
the representative of a specified coordinate it's not sufficient to get
simply the node where the pointer represent points to. This is because
within a LOD the parent node can also be combined with other nodes into
another parent node. If you want to known the representative in LOD x of
a coordinate you must follow the represent pointers until the lod
number of the node is greater than x (or the lod number is -1 - this means
this lod is not generated yet).
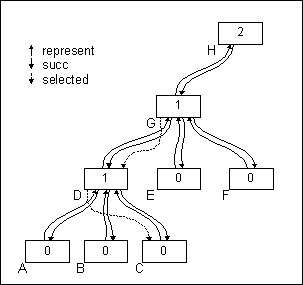
Consider you want to know the representative in LOD 1 of the coordinate
B of LOD 0.
In this case you must follow the represent pointer to D and than to G. At G you have to stop because the lod number of H is 2. The representative in LOD 1 of the coordinate B of LOD 0 is G. The representative in LOD 1 of A, C, E, F is also G.
Sometimes it is neccessary to known which coordinate in LOD y was selected as the representative. For this reason a selected pointer points from each parent node to the selected subnode. In this case you must follow the selected pointer until the lod number of the node is lesser than y or there no more subnodes. In the example above the selected coordinate in LOD 0 of the coordinate G is C.