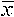 , die man durch Weglassen der Terme k+1-ter Ordnung und höher
erhält, nennt man den k-Jet von F bei
, die man durch Weglassen der Terme k+1-ter Ordnung und höher
erhält, nennt man den k-Jet von F bei
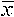 und wird mit
jk(F)(
und wird mit
jk(F)(
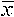 )
bezeichnet.
)
bezeichnet.
So kann man zum Beispiel sagen, daß der topologische Typ eines hyperbolischen Fixpunktes 1-Jet-determiniert ist, also die ganze Information über die Topologie steckt schon in den Termen erster Ordnung der Taylorentwicklung. Umgekehrt kann man feststellen, welcher k-Jet die Topologie eines nicht-hyperbolischen Fixpunktes vollkommen determiniert.