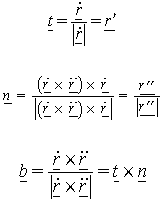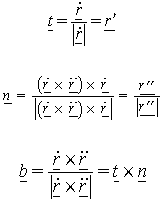Differentialgeometrie von Raumkurven
- Raumkurven
- Frenet-Frame
- Krümmung und Torsion
- Frenet-Formeln
Raumkurven
Kurven (= eindimensionale Linien, eindimensioanle Mannigfaltigkeiten)
im dreidimensionalen Raum werden meist in Parameterform dargestellt.
r(t) = x(t)i + y(t)j + z(t)k
Dabei ist t der laufende Parameter. Häufig werden Kurven nach der
Zeit parametrisiert (t), aber auch Parametrisierung nach der
Bogenlänge ist gebräuchlich. Diese wird mit meist mit s
bezeichnet.
Die Ableitungen nach t werden mit Punkten gekennzeichnet, die nach s
wie gewohnt mit Strichen.
Frenet-Frame
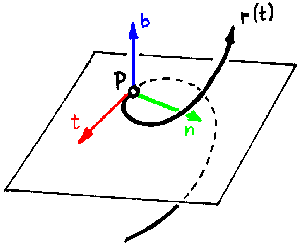
Das Frenet-Frame ist eine orthogonale Koordinatenbasis, die an jedem
Punkt der Kurve gesondert definiert ist (begleitendes Dreibein). Es
besteht aus dem Tangentialvektor t, dem Normalvektor n
und der Binormalen b.
t und n spannen die Schmiegebene der Kurve im
betrachteten Punkt auf. b steht normal auf diese Ebene und wird
i. a. so orientiert, daß t, n und b
ein Rechtssystem bilden.
Die drei Vektoren werden wie folgt definiert:
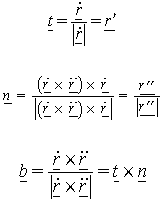
Krümmung und Torsion
In jedem Punkt der Kurve gibt es einen Kreis, der die Kurve dort
am besten approximiert (Krümmungskreis).
Die Krümmung K ist definiert
als der Reziprokwert des Radius dieses Kreises.
Je größer der Radius ist,
desto kleiner ist also die Krümmung.
Eine Gerade hat daher die Krümmung 0.
Es gilt: K = abs(r'')
Während die Krümmung angibt, wie stark die Kurve von einer
Geraden abweicht, gibt die Torsion an, wie stark
sich die Kurve aus der jeweiligen Schmiegebene "herausdreht"
(siehe Zeichnung oben bei Frenet-Frame)
Falls die Kurve (lokal) eine Gerade ist, ist die Schmiegebene nicht
eindeutig definiert.
Daher existieren auch unendlich viele Frenet-Frames, deren erster
Vektor in der Tangente liegt. Die Krümmung und die Torsion
sind in einem solchen Punkt gleich 0.
Frenet-Formeln
Die lokale Änderung des begleitenden Dreibeins hängt
natürlich eng mit dem Verlauf der Kurve im betrachteten Punkt
zusammen, d.h. mit Krümmung K und Torsion T:
t' = Kn
n' = -Kt + Tb
b' = -Tn
weiter zu den Literaturverweisen
zurück zu Eigenwert und -vektor
Mathematische Grundlagen Übersicht