Speaker: Hiroyuki Sakai
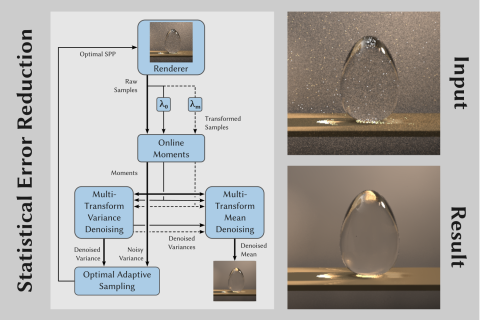
Denoising is an important post-processing step in physically based Monte Carlo (MC) rendering. While neural networks are widely used in practice, statistical analysis has recently become a viable alternative for denoising. In this paper, we present a general framework for statistics-based error reduction of both estimated radiance and variance.
Specifically, we introduce a novel denoising approach for variance estimates, which can either improve variance-aware adaptive sampling or provide additional input for image denoising in a cascaded manner.
Furthermore, we present multi-transform denoising: a general and efficient correction scheme for non-normal distributions, which typically occur in MC rendering. All these contributions combine to a robust denoising pipeline that does not require any pretraining and can run efficiently on current GPU hardware.
Our results show distinct advantages over previous denoising methods, especially in the range of a few hundred samples per pixel, which is of high practical relevance. Finally, we demonstrate good convergence behavior as the number of samples increases, providing predictable results with low bias that are free of hallucinated neural artifacts.
In summary, our statistics-based algorithms for adaptive sampling and denoising deliver fast, consistent, low-bias variance and radiance estimates.