ManifoldMusic is a Windows application for music visulization through Manifold Harmonics, developed as a lab exercise for the course 'Visualisation 2' at the Vienna University of Technology.

This is how it works: You load a mesh in .obj format (File->Open mesh); we recommend you use one of those that we packed into the binary-distribution, because the meshes must fulfill certain requirements for the application to work properly. Then you can load an audio file (almost any format) and watch the mesh dancing :)
NOTE: due to some extensive computations the loading of the mesh can take some time, depending on the number of vertices up to a minute.

The behaviour of the mesh can be influenced by the sliders on the right side of the window: You can influence the smoothness of movement, the number of frequencies used to reconstruct the mesh (you could interpret this as something like 'level of detail') and the influence of the sound on the low, middle and high frequencies of the mesh (more information below).

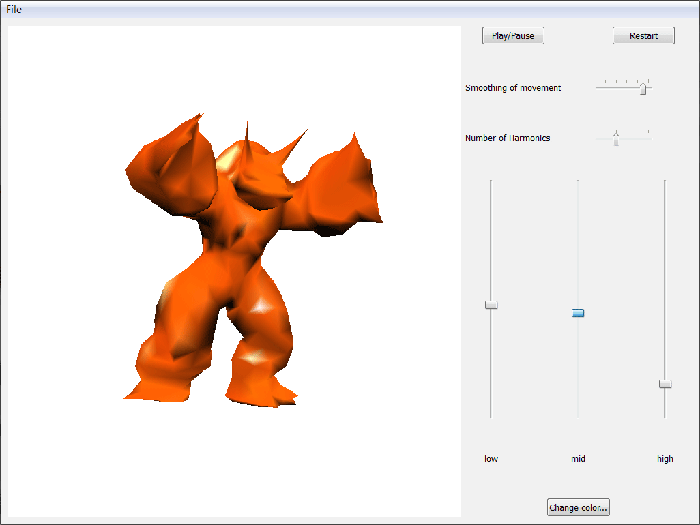
Manifold Harmonics?

We know that images and audio signals can be transformed to frequency space in order to perform filtering operations that would be very hard to do in the original space. Now you can also do that with meshes!

If you transform a mesh to frequency space you end up with a set of what we call 'Manifold Harmonics'. Now you can deliberately filter them, amplify some harmonics or cut out others. If the mesh is then recreated out of the filtered harmonics, we get results like these (screenshots of a demo applet made by these guys, the graph in the bottom left corner shows the applied filter function):

In our ManifoldMusic application we 'link' the harmonics of the mesh to the harmonics of a song, i.e. our filter is derived from the song's harmonic amplitudes in realtime.

So how exactly does it work?

The whole process is described in this paper. But to put it in a nutshell, this is what we did:

1. Compute the Laplace-De Rham operator Δ
If your mesh has n vertices, Δ is an nxn matrix with coefficients defined as follows:

Here area_i of vertex v_i is the area of a polygon defined by the edge midpoints m_k and the face barycenters c_l (1). Angles β_ij and β'_ij are the angles opposite to the edge connecting vertices v_i and v_j (2). If v_i and v_j are not adjacent, Δ_ij is set to 0.

2. Compute the Manifold Harmonics Basis (MHB)
This is 'simply' done by computing the eigenvectors of the Laplace-De Rham operator. Then we put them in ascending order with respect to their eigenvalues, because the square root of the eigenvalues indicates the frequency that they are responsible for. The MHB is again an nxn matrix, where the columns are the ordered eigenvectors. We call the columns H_k and the rows H_i.

3. Compute the Manifold Harmonics Transformation (MHT)
We define vectors X,Y and Z as vectors which contain all the x/y/z coordinates of our original mesh and X^t,Y^t and Z^t as vectors which contain the coordinates of the transformed mesh. Then we can calculate the MHT as follows:
X^t_k = X · H_k
Y^t_k = Y · H_k
Z^t_k = Z · H_k
(" · " is a scalar product)

4. Apply a filter
Now we can filter the mesh by element-wise multiplying the MHT with a filter function Φ:
X^filtered_k = X^t_k · Φ_k
Y^filtered_k = Y^t_k · Φ_k
Z^filtered_k = Z^t_k · Φ_k
As our goal is to visualize music, Φ is created on basis of the harmonics of an audio stream.

5. Transform the mesh back to euclidean space
For backtransformation we must use the inverse MHB or, simply spoken, multiply with the rows H_i instead of the columns H_k: X^new_i = H_i · X^filtered
Y^new_i = H_i · Y^filtered
Z^new_i = H_i · Z^filtered

That's it! We now have new positions for our vertices and can re-draw the scene.
Steps 1-3 have to be performed only once, steps 4 and 5 must be performed every frame!

Implementation details

The graphical user interface was created with Qt.

For the computation of the Laplace-De Rham operator you need lots of neighborhood and topology information. Not only you have to find the neighbors of a vertex, you also must be able to travers them in a specific order. Using just lists of vertices and face indices, this is quite impossible. A good solution is to generate a half edge data structure. We used OpenMesh for this task.
Along with OpenMesh come a couple of example applications, including a neat Qt-based mesh viewer; we used its sourcecode as a basis to our GUI and rendering environment.

Next interesting thing is the computation of eigenvectors of big matrices. Luckily Eigen does a pretty good job here. Anyhow, the algorithm Eigen uses has a runtime of O(n³) for an nxn matrix, so processing meshes with a high number of vertices in a reasonable time is kind of a problem.

For audio processing, that is, playback of songs and harmonic analysis, we used fmod.