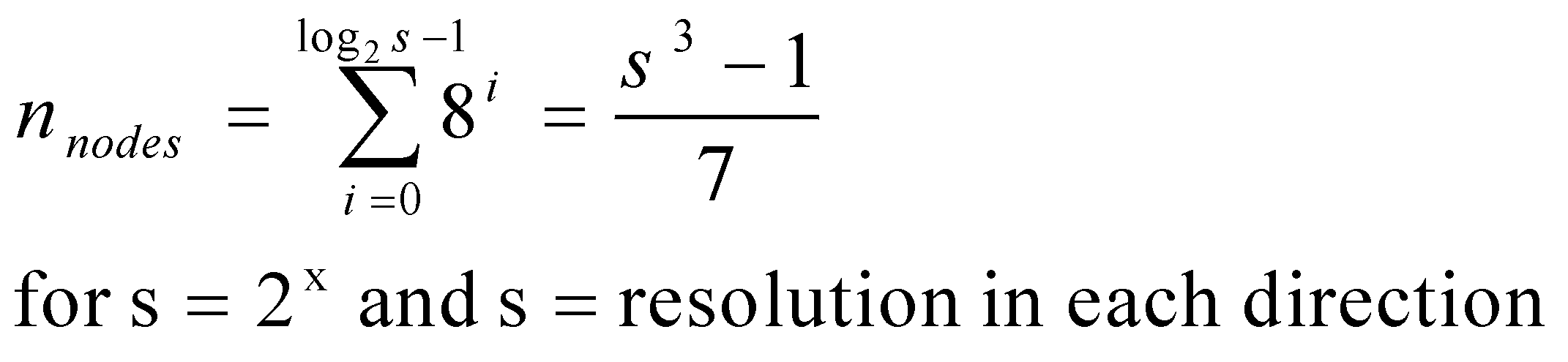Octree
(by J. Eder 9225396)
What is an Octree?
Using an Octree
Types of Octrees
What does it represent?
How is it managed?
How to structure Octree-structures
Pointerless full Octree
Traditional design of Pointer Octrees
Branch-On-Need-Octree
What is an Octree ?
(First I have to say, that it was discussed, if an Octree which doesn't
branchs in all directions in the same moment is not an Octree: this paper
doesn't matter when to branch, it just assumes that you have not less than
zero and not more than eight child-nodes and in any meaning its matter
is volumes)
Because many volume data-sets are very large it isn’t possible to interactively
render such a scene. The implementation of hierarchical data structures
could make this better. An Octree is such a hierarchical data structure.
It is a kind of a tree, which nodes (except the leaves) each has max.
eight child-nodes. Mostly the nodes represent volume-pieces which are further
divided into max. eight “Octants” which are represented by the child-nodes.
The Octants mostly are regular, but also irregular shapes are imaginable.
If the maximum resolution is reached at one node, it’s a leave of the tree.
If the leaves of a node have exactly the same attributes, it is possible
to reduce them to a node. This is called condensation.
Using an octree
Usually an Octree represents a volume, but of course it is possible to
use it for different applications, such as to represent spatial relationships
of geometrical objects. But the most common use is to represent a volume.
Some calculations work very much faster if they can be performed on condensed
node. Of course each node "carries" a type of information in it. If its
job is just to represent if the "voxel" is there or not it's a boolean
data type. On the other hand it is arguable to store a complete set of
values, for instance dense values, temperature values and the further.
This data type is non boolean.
Type of Octrees
There are several methods to distinguish the "family" of octrees, but I
would say the best are:
What does it represent?
How is it managed?
What does it represent?
There you can distinguish two mainly different types of information: Boolean
and Non-Boolean Information. At the boolean information there's just the
information saved, if the volume is interesting (BLACK) or not (WHITE).
This binary decision only works clear for leaves, but for any ancestor-nodes
there can be a third possibility: Some of the nodes could be BLACK and
some of the nodes could be WHITE, then these ancestor-nodes are called
"GRAY".
With Non-Boolean data it's not so easy: The information can be any
value and its the more unlikely that you can condense the nodes than the
more possibilities the attributes of the nodes have to get set. Therefore
mostly all ancestor-nodes are gray nodes, which means that cannot be condensed
and for nearly all discrete volume points you need its ancestors, which
need also memory. This can be enhanced until about the double amount.
How is it managed?
There are any positibilities to implement an octree, the mostly common
approaches are pointer based and with array (pointerless). The pointerbased
octrees have for each child node a pointer which shows the position of
the child. Sometimes there is also a pointer to the ancestor. (Of course
not to forget the attributes of the node) If a gray node is defined it
means, that all pointers are filled and this of course takes memory. The
next approach is the linear octree which works (nearly) without pointers.
If you decide, always to make a "full" octree (all ancestors have all child-nodes),
you exactly know for a given size of a volume the amount of nodes in one
hierarchical plane. Thats why it's directly possible to calculate the address
of the wanted node. This method is very memory effortable, because it assumes
a full octree.
If the path is saved, how to get from the root to the leaf, it
needs not a full octree. Each node now possess' a key which describes to
take which turn-off. These keys can be accessed through an array or a Hash-table.
How to structure Octree-structures
If you are working with trees it's hard enough to remember the correct
pointer for the wanted child and not to accidentally exchange it. But with
octrees is really tricky. That's why we should consider a name-giving convention.
It's called the ZYX-convention. In this convention you take the binary
number of 0-7 to describe the nodes. Then you say: first bit=Z-Coordinate,
second bit is Y-Coordinate, third bit is X-Coordinate. For each of these
coordinates you say "less" half or "greater" half (in coordinate direction)
and for less you say 0 and for greater you say 1.
Pointerless full Octree
In a full Octree each node has exactly eight children for each ancestor.
Therefore you can directly calculate the total number of nodes.
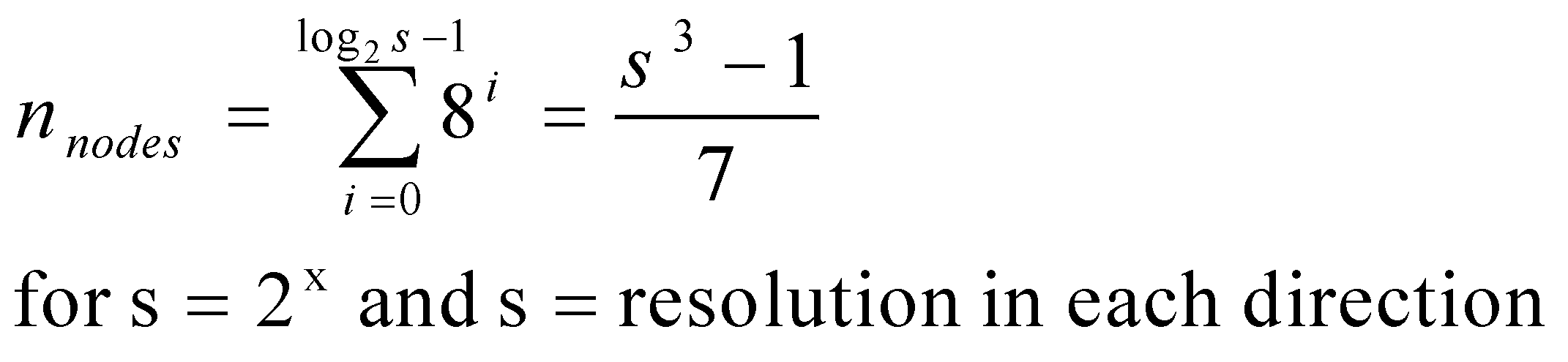
It is a regular structure and therefore the adress of the node can
be directly calculated. It cost much memory ( for 320x320x40 you need about
40 Mill words) and therefore the traditional design is with pointers.
Traditional design of Pointer Octrees
Each ancestor-node has eight pointers which can be empty or can point
to the child-node. It works with the "even-subdivision strategy". This
means, that each range is devided in nearly similar parts and the child
nodes nearly exactly describe the same volume. But the disadvantage is
described below with an example of 16x8x4 :
|
X
|
Y
|
Z
|
|
16
|
8
|
4
|
|
8,8
|
4,4
|
L,L
|
|
4,4,4,4
|
L,L,L,L
|
|
|
L,L,L,L,L,L,L,L
|
|
|
The tree is branching seperated in all dimensions which means that the
lowest level the leaves (the "L"s) are not efficient because all have much
Y and Z informations equal to another. Additionally they are the most.
Branch-on-Need Octree
The basic idea is, that the tree is only branching if "necessary" trying
branching similar to the power of 2. This is realized by dividing at that
moment at the binary number of the range is losing its leftmost bit. That
works like following: You write down the binary numbers of the ranges which
are the differences of their "upper" and their "lower" limits. Then you
write all leading zeros you need that you have the same number of digits
of all dimensions. You now only branch in that dimensions which have a
"1" in their leftmost bit. For example you have (16/15/8) or (10000/01111/01000):
It is branching only in the X direction. You can determin the childs ranges
just for the "upper" by simply removing the leftmost 1. It results in 0000,
which means "no further branch". The "lower" child you just take as "1"s
in the number of the number of digits of the remaining "upper" range. The
"lower" child has 1111 which means it now is a "power"-node which means
it branches in that dimension down for all nodes (like the power of 2:
15-7-3-1).
(Source: ACM Transactions on Graphical, Vol.11 No3,July '92)