Raphael Fuchs, Ronald Peikert, Helwig HauserORCID iD, Filip Sadlo, Philipp Muigg
Parallel Vectors Criteria for Unsteady Flow Vortices
TVCG, 14(3):615-626, May 2008. [Paper]

Information

  • Publication Type: Journal Paper (without talk)
  • Workgroup(s)/Project(s):
  • Date: May 2008
  • Journal: TVCG
  • Number: 3
  • Volume: 14
  • Pages: 615 – 626
  • Keywords: Time-Varying Data Visualization, Vortex Feature Detection

Abstract

Feature-based flow visualization is naturally dependent on feature extraction. To extract flow features, often higher-order properties of the flow data are used such as the Jacobian or curvature properties, implicitly describing the flow features in terms of their inherent flow characteristics (e.g., collinear flow and vorticity vectors). In this paper we present recent research which leads to the (not really surprising) conclusion that feature extraction algorithms need to be extended to a time-dependent analysis framework (in terms of time derivatives) when dealing with unsteady flow data. Accordingly, we present two extensions of the parallel vectors based vortex extraction criteria to the time-dependent domain and show the improvements of feature-based flow visualization in comparison to the steady versions of this extraction algorithm both in the context of a high-resolution dataset, i.e., a simulation specifically designed to evaluate our new approach, as well as for a real-world dataset from a concrete application.

Additional Files and Images

Additional images and videos

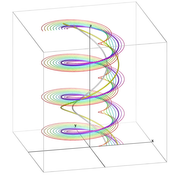
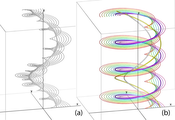Figure1: Streamlines and pathlines in a model of a rotating vortex rope. (a) The vortex core line based on streamlines (according to Sujudi and Haimes) is shown as a thick grey tube (it is the only grey line which also is a helix). (b) The vortex core line based on pathlines (shown in yellow on the right) has the same pitch but a larger radius (it is the only helical pathline, shown in thick magenta). Figure1: Streamlines and pathlines in a model of a rotating vortex rope. (a) The vortex core line based on streamlines (according to Sujudi and Haimes) is shown as a thick grey tube (it is the only grey line which also is a helix). (b) The vortex core line based on pathlines (shown in yellow on the right) has the same pitch but a larger radius (it is the only helical pathline, shown in thick magenta).
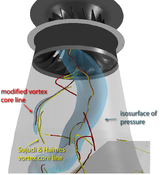Figure2: For the vortex rope in the depicted dataset, iso-values of pressure give good insight on where the vortex core line is located. We can clearly see how the yellow core line (extracted using the classical approach of Sujudi and Haimes deviates from the center of pressure isosurface. The modification to time derivative aware extraction of the vortex coreline improves the results visibly. Figure2: For the vortex rope in the depicted dataset, iso-values of pressure give good insight on where the vortex core line is located. We can clearly see how the yellow core line (extracted using the classical approach of Sujudi and Haimes deviates from the center of pressure isosurface. The modification to time derivative aware extraction of the vortex coreline improves the results visibly.
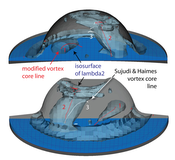Figure3: We compare the vortex core lines found by the original method of Sujudi and Haimes and the modified version. Two views of the same timestep show the benefits of the modification. Both views show the same vortex core line and isosurface. (1) In one case the original method does not detect one vortex core at all. (2) The time-aware modification traverses the full length of the vortex core and continues into the region of strong turbulence at the top of the cylinder. (3) The original vortex core line leaves the core region of the vortex and vanishes in a substantial portion of the vortex region. Figure3: We compare the vortex core lines found by the original method of Sujudi and Haimes and the modified version. Two views of the same timestep show the benefits of the modification. Both views show the same vortex core line and isosurface. (1) In one case the original method does not detect one vortex core at all. (2) The time-aware modification traverses the full length of the vortex core and continues into the region of strong turbulence at the top of the cylinder. (3) The original vortex core line leaves the core region of the vortex and vanishes in a substantial portion of the vortex region.
Figure4: Comparison of acceleration vector magnitudes: The scatterplots show that the magnitudes of the two variants of the acceleration vectors can differ significantly in the crucial timesteps, i.e., timesteps of major changes over time, after ignition (we have normalized the magnitudes such that the center of gravity corresponds to the origin). Figure4: Comparison of acceleration vector magnitudes: The scatterplots show that the magnitudes of the two variants of the acceleration vectors can differ significantly in the crucial timesteps, i.e., timesteps of major changes over time, after ignition (we have normalized the magnitudes such that the center of gravity corresponds to the origin).
Figure5: We compare the computed corelines with respect to lambda2 and equivalence ratio. (a) The modified algorithm detects two vortex core lines (red) whereas the original version only detects the main vortex core line (white). (b) An isosurface of equivalence ratio at 0.7 containing the region of optimal mixing. (c) The surface containing the region of equivalence ratio of 0.5 and lambda2< -1000$. Figure5: We compare the computed corelines with respect to lambda2 and equivalence ratio. (a) The modified algorithm detects two vortex core lines (red) whereas the original version only detects the main vortex core line (white). (b) An isosurface of equivalence ratio at 0.7 containing the region of optimal mixing. (c) The surface containing the region of equivalence ratio of 0.5 and lambda2< -1000$.
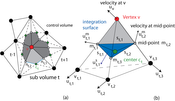Figure6: Gradient estimation at a vertex (red) using the Green-Gauss theorem requires to estimate cell center velocities and mid-point velocities. (a) The surrounding surface uses cell centers (green) and mid-points (gray). (b) In this detail illustration of the lighter gray section from (a) we see the full configuration for a single surrounding tetrahedron. Figure6: Gradient estimation at a vertex (red) using the Green-Gauss theorem requires to estimate cell center velocities and mid-point velocities. (a) The surrounding surface uses cell centers (green) and mid-points (gray). (b) In this detail illustration of the lighter gray section from (a) we see the full configuration for a single surrounding tetrahedron.
Image
Image

Additional files

Paper
Paper

Weblinks

No further information available.

BibTeX

@article{fuchs_raphael_2007_par,
  title =      "Parallel Vectors Criteria for Unsteady Flow Vortices",
  author =     "Raphael Fuchs and Ronald Peikert and Helwig Hauser and Filip
               Sadlo and Philipp Muigg",
  year =       "2008",
  abstract =   "Feature-based flow visualization is naturally dependent   on
               feature extraction. To extract flow features, often
               higher-order   properties of the flow data are used such as
               the Jacobian or   curvature properties, implicitly
               describing the flow features in   terms of their inherent
               flow characteristics (e.g., collinear flow   and vorticity
               vectors). In this paper we present recent research   which
               leads to the (not really surprising) conclusion that feature
               extraction algorithms   need to be extended to a
               time-dependent analysis framework (in terms   of time
               derivatives) when dealing with unsteady flow data.  
               Accordingly, we present two extensions of the parallel
               vectors based vortex   extraction criteria to the
               time-dependent domain and show the improvements of  
               feature-based flow visualization in comparison to the  
               steady versions of this extraction algorithm both in the
               context of   a high-resolution dataset, i.e., a simulation
               specifically designed   to evaluate our new approach, as
               well as for a real-world dataset   from a concrete
               application.",
  month =      may,
  journal =    "TVCG",
  number =     "3",
  volume =     "14",
  pages =      "615--626",
  keywords =   "Time-Varying Data Visualization, Vortex Feature Detection",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2008/fuchs_raphael_2007_par/",
}